Normality Test

library(tidyverse)
library(rstatix)
library(ggpubr)

References

Explore Data

glimpse(ToothGrowth)
#> Rows: 60
#> Columns: 3
#> $ len  <dbl> 4.2, 11.5, 7.3, 5.8, 6.4, 10.0, 11.2, 11.2, 5.2, 7.0, 16.5, 16.5,…
#> $ supp <fct> VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, V…
#> $ dose <dbl> 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0, 1.0, 1.0, …
skimr::skim(ToothGrowth)
Data summary
Name ToothGrowth
Number of rows 60
Number of columns 3
_______________________
Column type frequency:
factor 1
numeric 2
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
supp 0 1 FALSE 2 OJ: 30, VC: 30

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
len 0 1 18.81 7.65 4.2 13.07 19.25 25.27 33.9 ▅▃▅▇▂
dose 0 1 1.17 0.63 0.5 0.50 1.00 2.00 2.0 ▇▇▁▁▇

Normality Check

Objective

We want to test if the variable len (tooth length) is normally distributed.

Visual Method

Histogram

ToothGrowth %>% 
  ggplot(aes(len)) +
  geom_histogram()
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.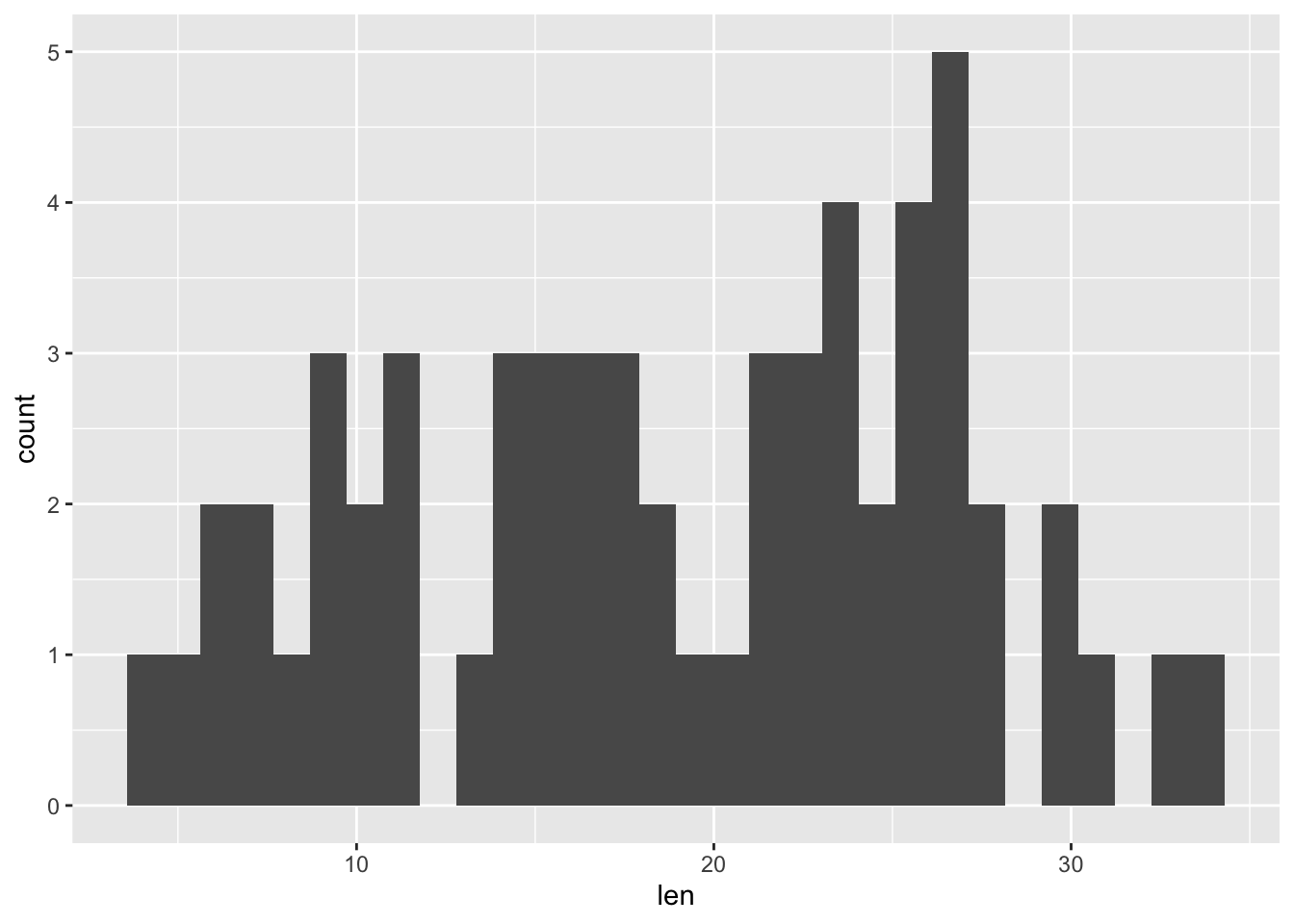

Density

ggdensity(ToothGrowth$len, fill = "lightgray")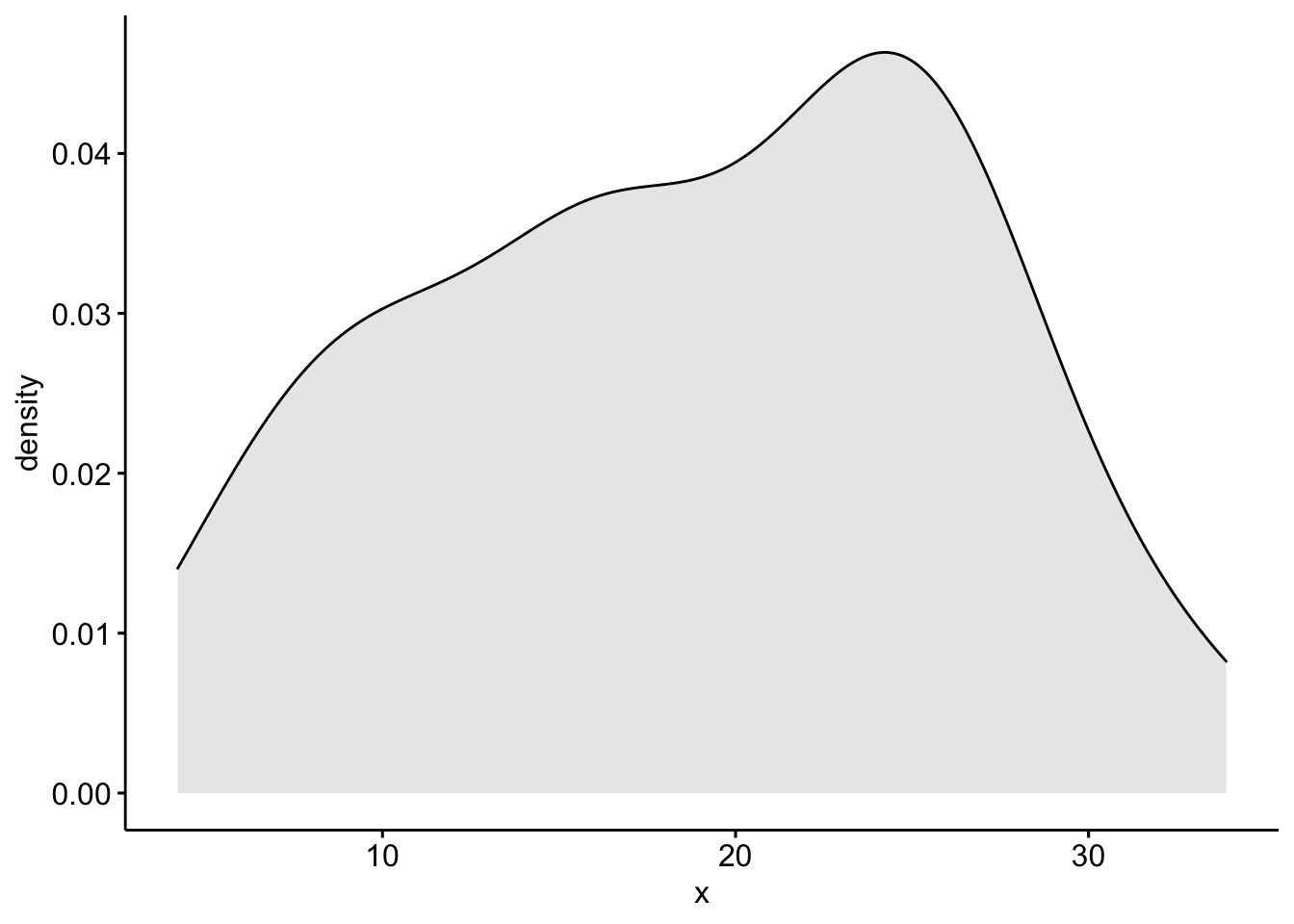

QQ Plot

ggqqplot(ToothGrowth$len)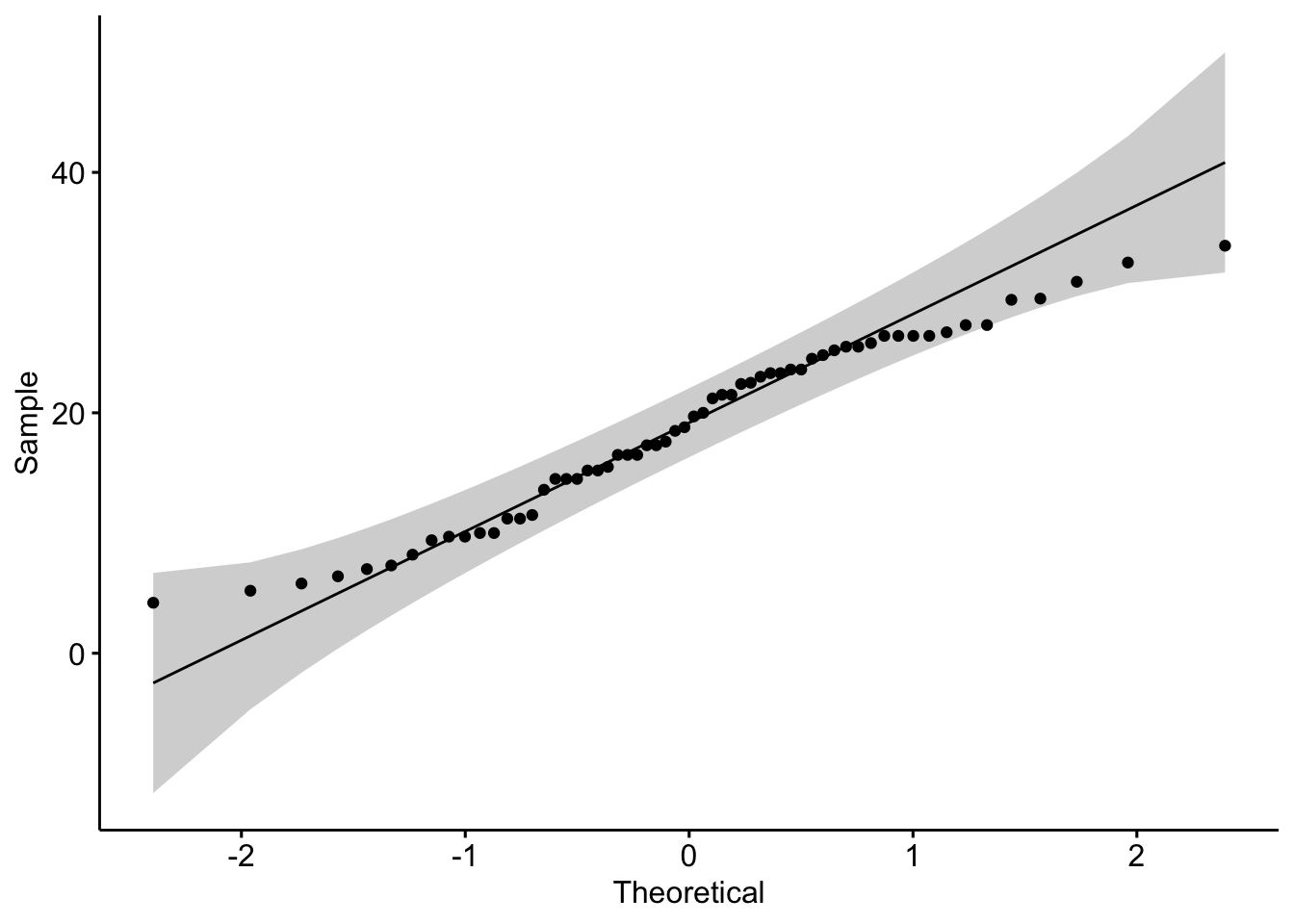

ToothGrowth %>% 
  ggplot(aes(sample = len)) +
  geom_qq() +
  geom_qq_line()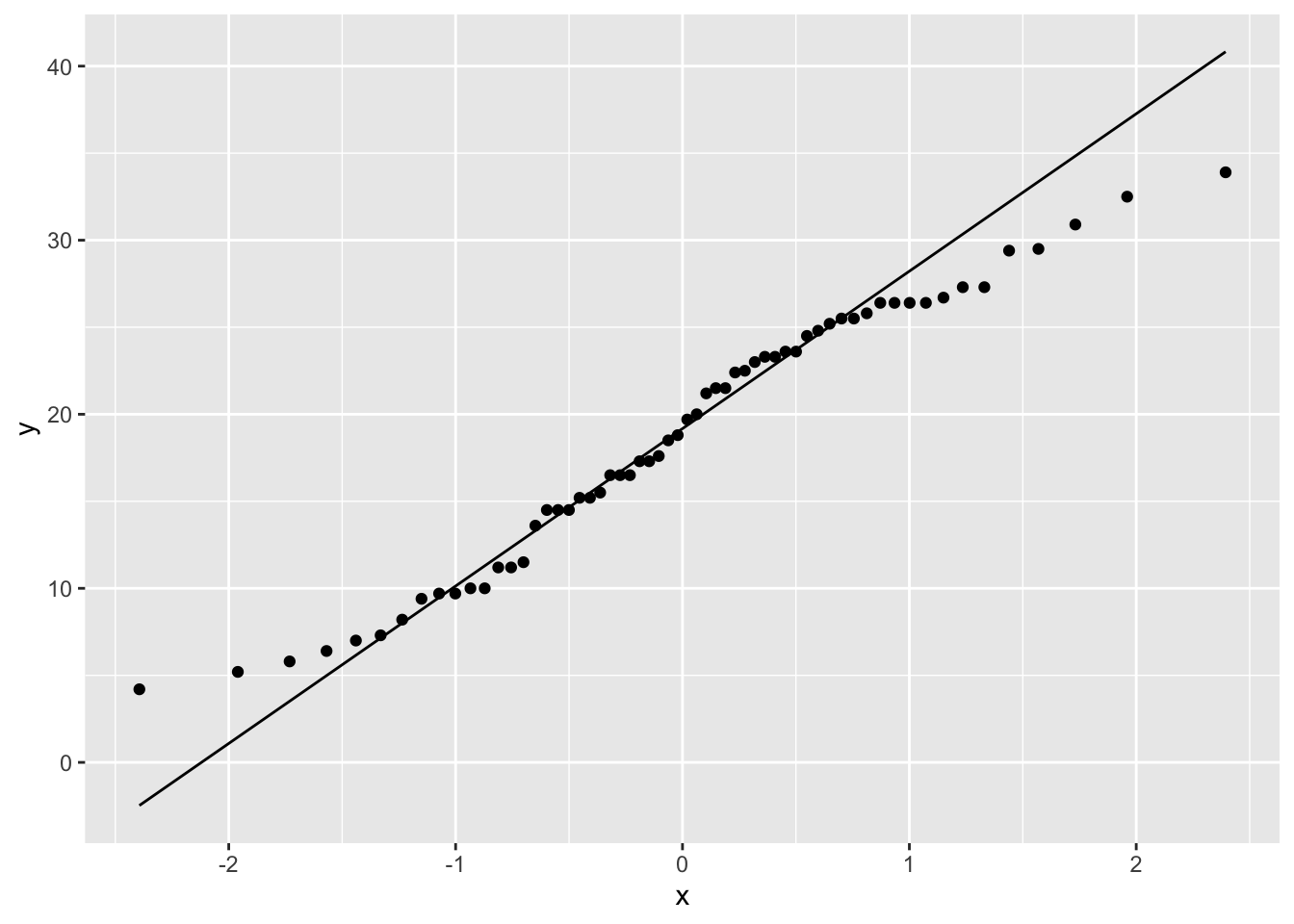

Shapiro-Wilk’s normality test

Hypothesis

\(H_0\) = “sample distribution is normal”

One Variable

shapiro.test(ToothGrowth$len)
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  ToothGrowth$len
#> W = 0.96743, p-value = 0.1091

Or

ToothGrowth %>% shapiro_test(len)
#> # A tibble: 1 × 3
#>   variable statistic     p
#>   <chr>        <dbl> <dbl>
#> 1 len          0.967 0.109

P-value > 0.05; implying that the distribution of the data are not significantly different from normal distribution; therefore, we can assume normality.

Grouped Data

ToothGrowth %>%
  group_by(dose) %>%
  shapiro_test(len)
#> # A tibble: 3 × 4
#>    dose variable statistic     p
#>   <dbl> <chr>        <dbl> <dbl>
#> 1   0.5 len          0.941 0.247
#> 2   1   len          0.931 0.164
#> 3   2   len          0.978 0.902