Causal Inference (DAG)

Code adapted from r-causal (CH.5)

library(gtsummary)
library(patchwork)
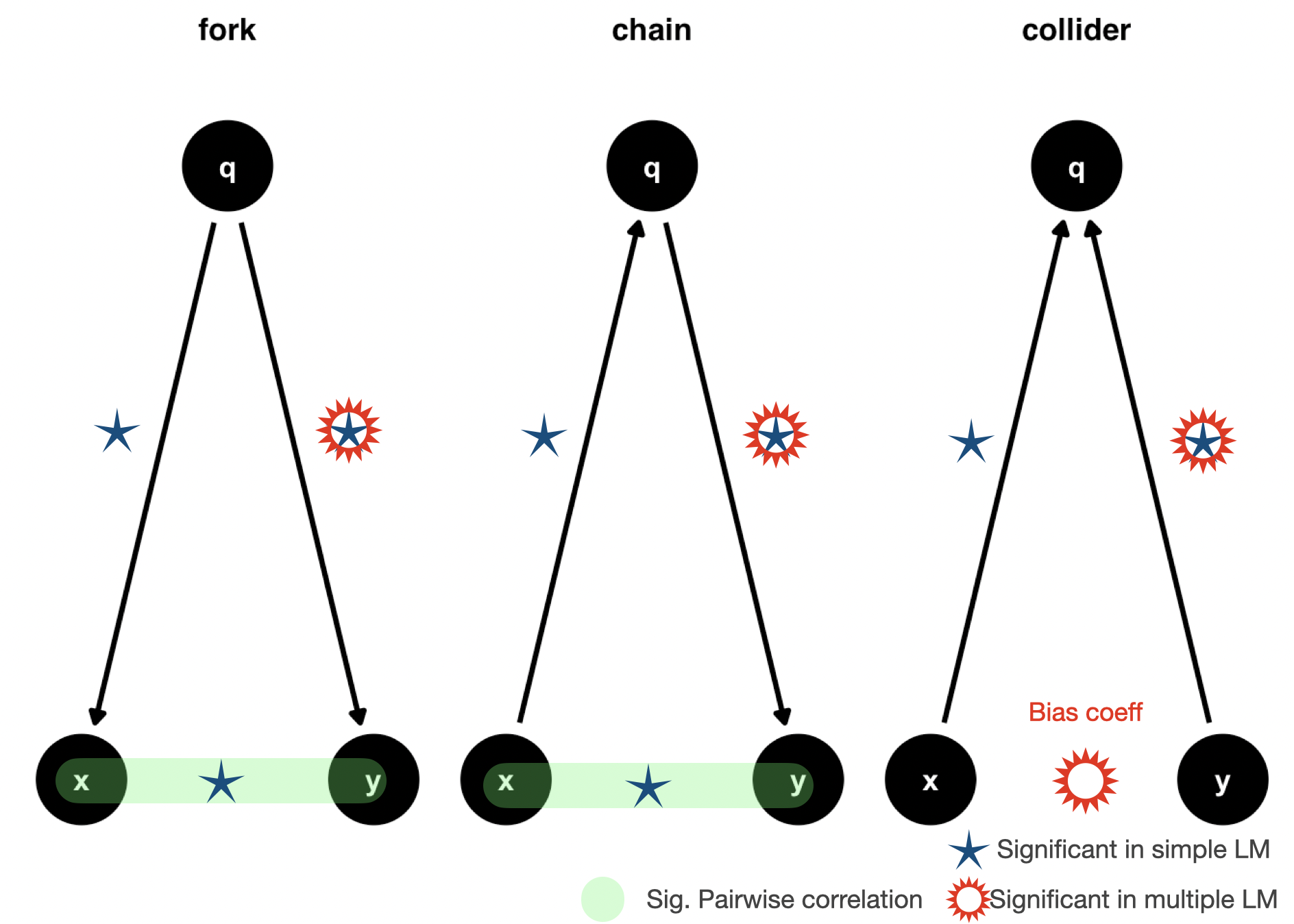
library(correlation)

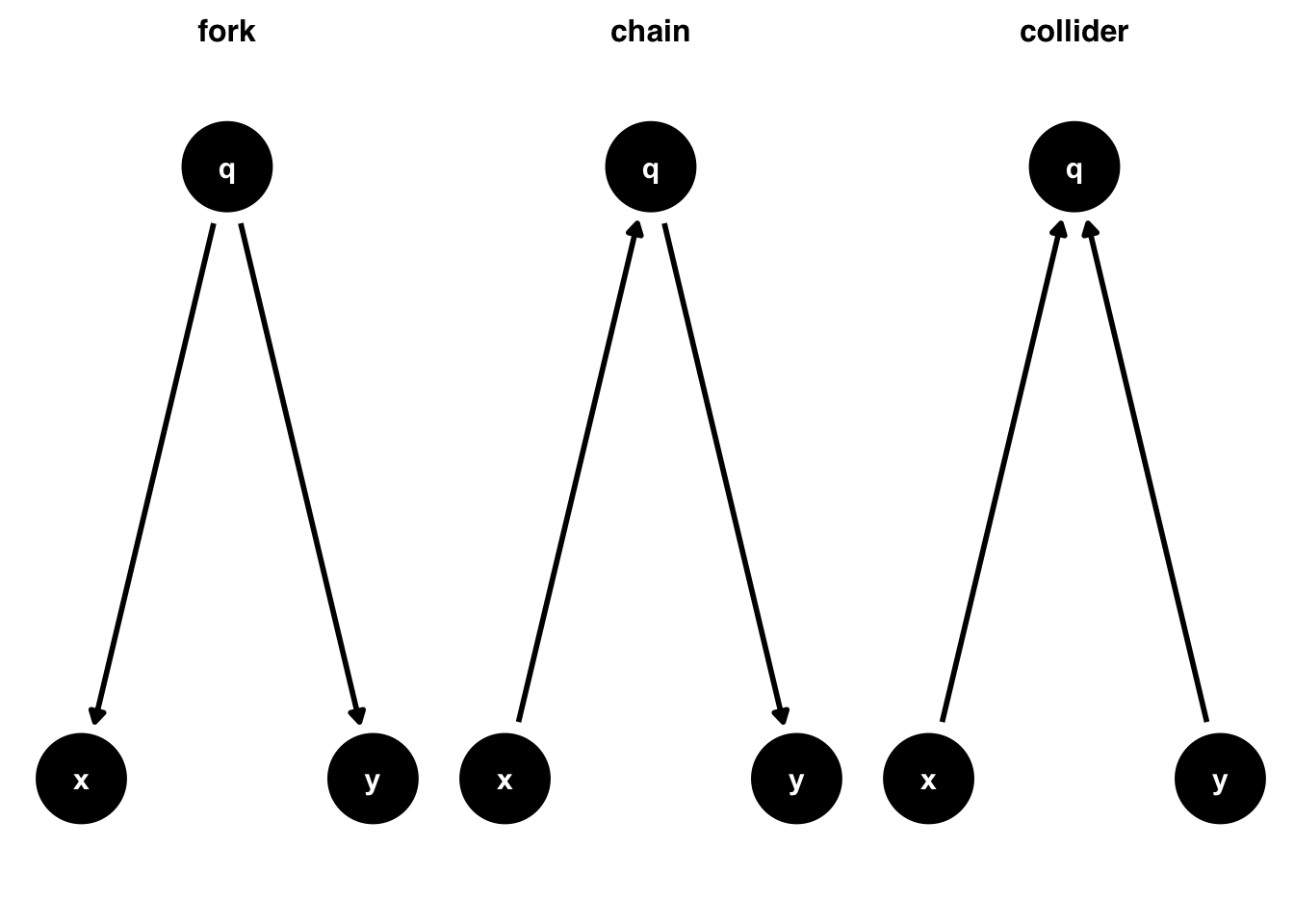
Fork (Confounder)

Sim Data

set.seed(123)
n <- 1000

q <- rbinom(n, size = 1, prob = .35)
x <- 2 * q + rnorm(n)
y <- -3 * q + rnorm(n)

confounder_data <- tibble(x, y, q = as.factor(q))

Plot

Code

p1 <- confounder_data |>
  ggplot(aes(x, y)) +
  geom_point(alpha = .2) +
  geom_smooth(method = "lm", se = FALSE, color = "black") +
  facet_wrap(~"not adjusting for `q`\n(biased)")

p2 <- confounder_data |>
  ggplot(aes(x, y, color = q)) +
  geom_point(alpha = .2) +
  geom_smooth(method = "lm", se = FALSE) +
  facet_wrap(~"adjusting for `q`\n(unbiased)")

p1 + p2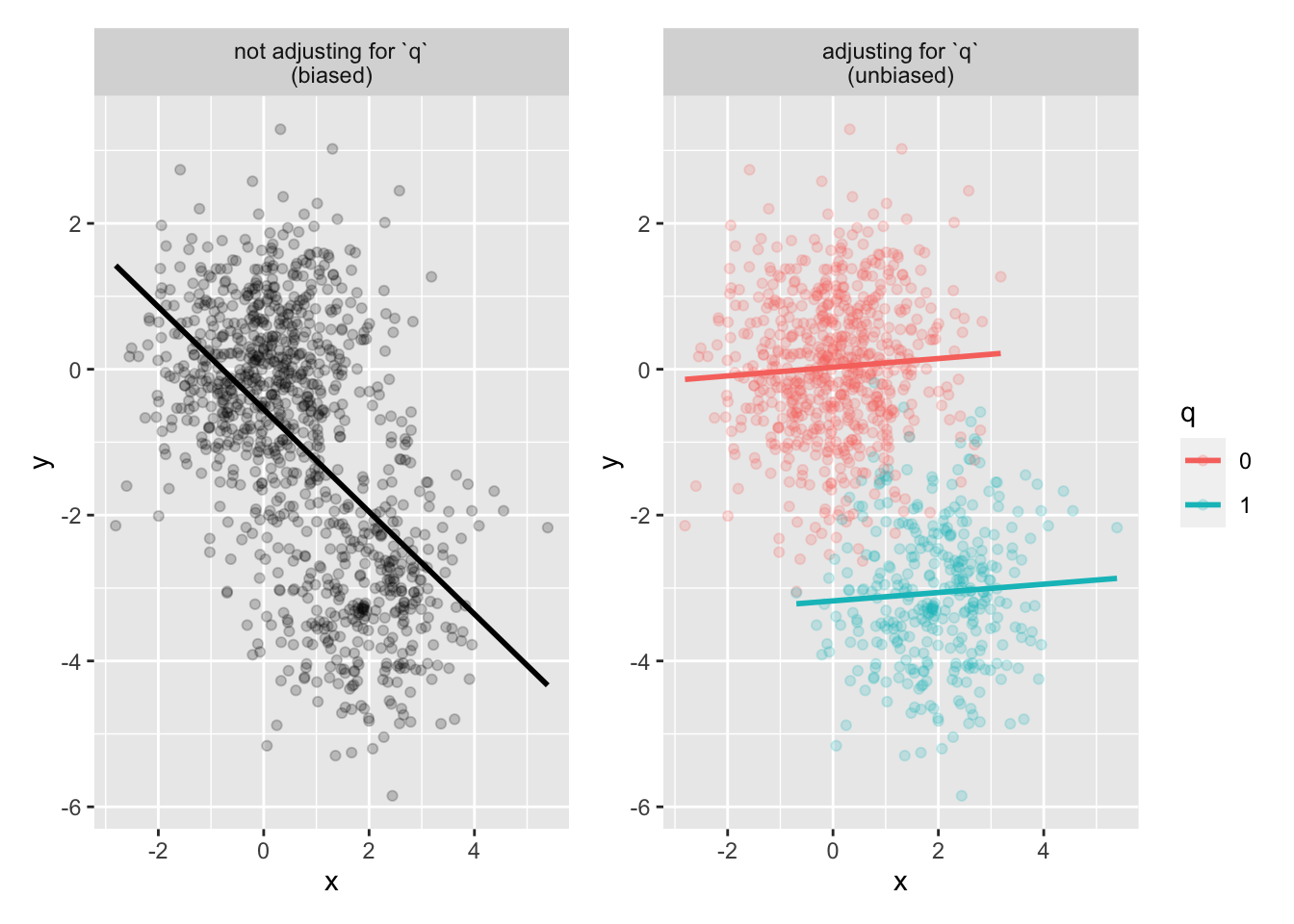

Corr

lares::corr_cross(confounder_data)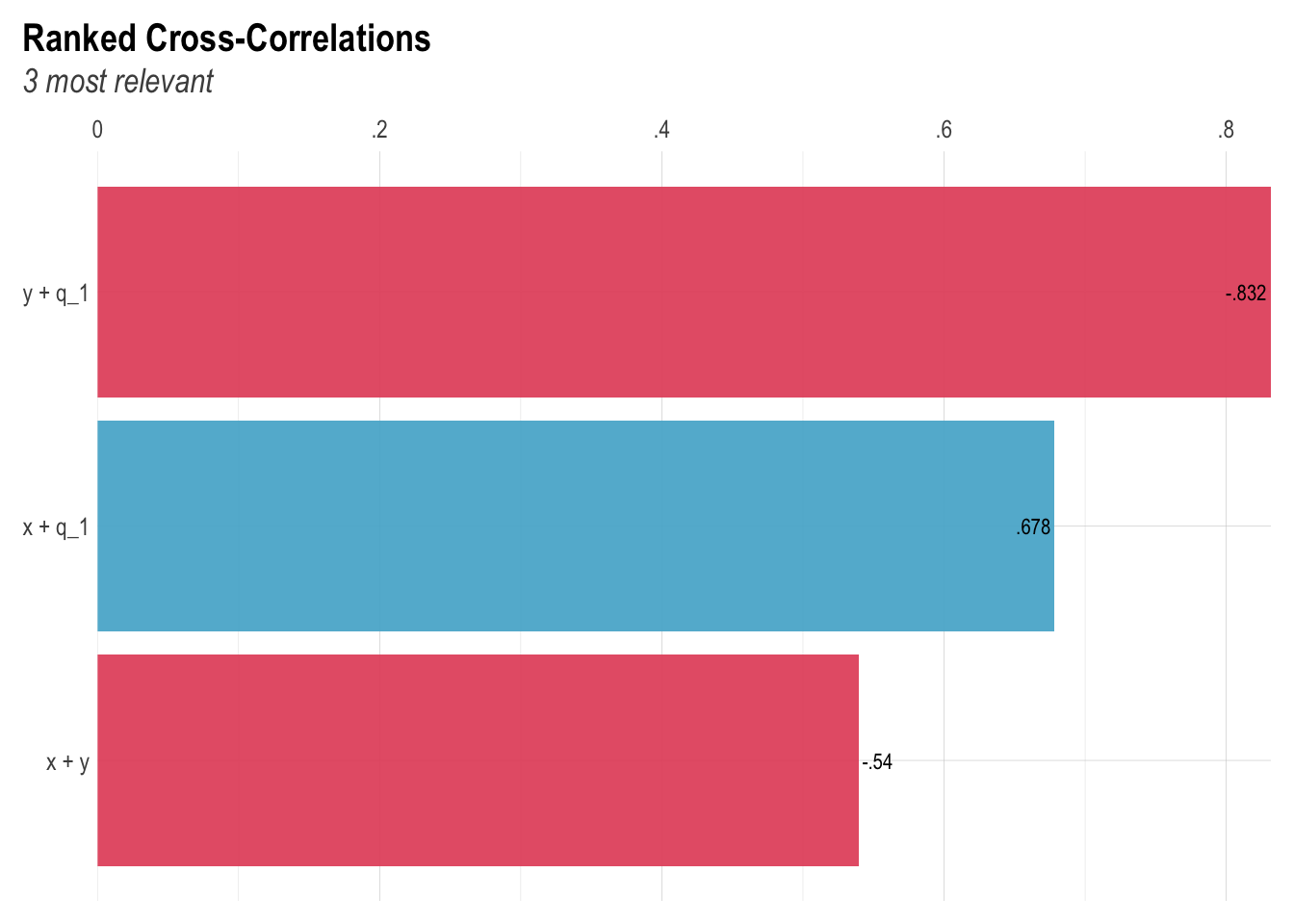

correlation(confounder_data)

# Correlation Matrix (pearson-method)

Parameter1 | Parameter2 |     r |         95% CI | t(998) |         p
---------------------------------------------------------------------
x          |          y | -0.54 | [-0.58, -0.49] | -20.26 | < .001***

p-value adjustment method: Holm (1979)
Observations: 1000

Model

# Not Adjust
## y ~ x
confounder_data.fit.y_x <- lm(y ~ x, data = confounder_data)
## y ~ q 
confounder_data.fit.y_q <- lm(y ~ q, data = confounder_data)
## x ~ q
confounder_data.fit.x_q <-  lm(x ~ q, data = confounder_data)

# Adjusted: y ~ x + q 
confounder_data.fit.y_xq <- lm(y ~ x + q, data = confounder_data)

Code

confounder_data.fit.tbls <- 
  list(
    y_x = confounder_data.fit.y_x,
    y_q = confounder_data.fit.y_q,
    x_q = confounder_data.fit.x_q,
    y_xq = confounder_data.fit.y_xq
  ) |> 
  map(tbl_regression_custom)
  
confounder_data.fit.tbls |> 
tbl_merge(
  tab_spanner = c("**y ~ x**", "**y ~ q**", "**x ~ q**", "**y ~ x + q**")
  )

Characteristic	y ~ x			y ~ q			x ~ q			y ~ x + q
Characteristic	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value
x	-0.70	-0.77, -0.63	<0.001							0.06	0.00, 0.12	0.059
q
0				—	—		—	—		—	—
1				-3.1	-3.2, -3.0	<0.001	1.9	1.8, 2.1	<0.001	-3.2	-3.4, -3.0	<0.001
¹ CI = Confidence Interval

Chain (Mediator)

Sim Data

set.seed(123)
x <- rnorm(n)

linear_pred <- 2 * x + rnorm(n)
prob <- 1 / (1 + exp(-linear_pred))
q <- rbinom(n, size = 1, prob = prob)
y <- 2 * q + rnorm(n)

mediator_data <- tibble(x, y, q = as.factor(q))

Plot

Code

p1 <- mediator_data |>
  ggplot(aes(x, y)) +
  geom_point(alpha = .2) +
  geom_smooth(method = "lm", se = FALSE, color = "black") +
  facet_wrap(~"not adjusting for `q`\n(total effect)")

p2 <- mediator_data |>
  ggplot(aes(x, y, color = q)) +
  geom_point(alpha = .2) +
  geom_smooth(method = "lm", se = FALSE) +
  facet_wrap(~"adjusting for `q`\n(direct effect)")

p1 + p2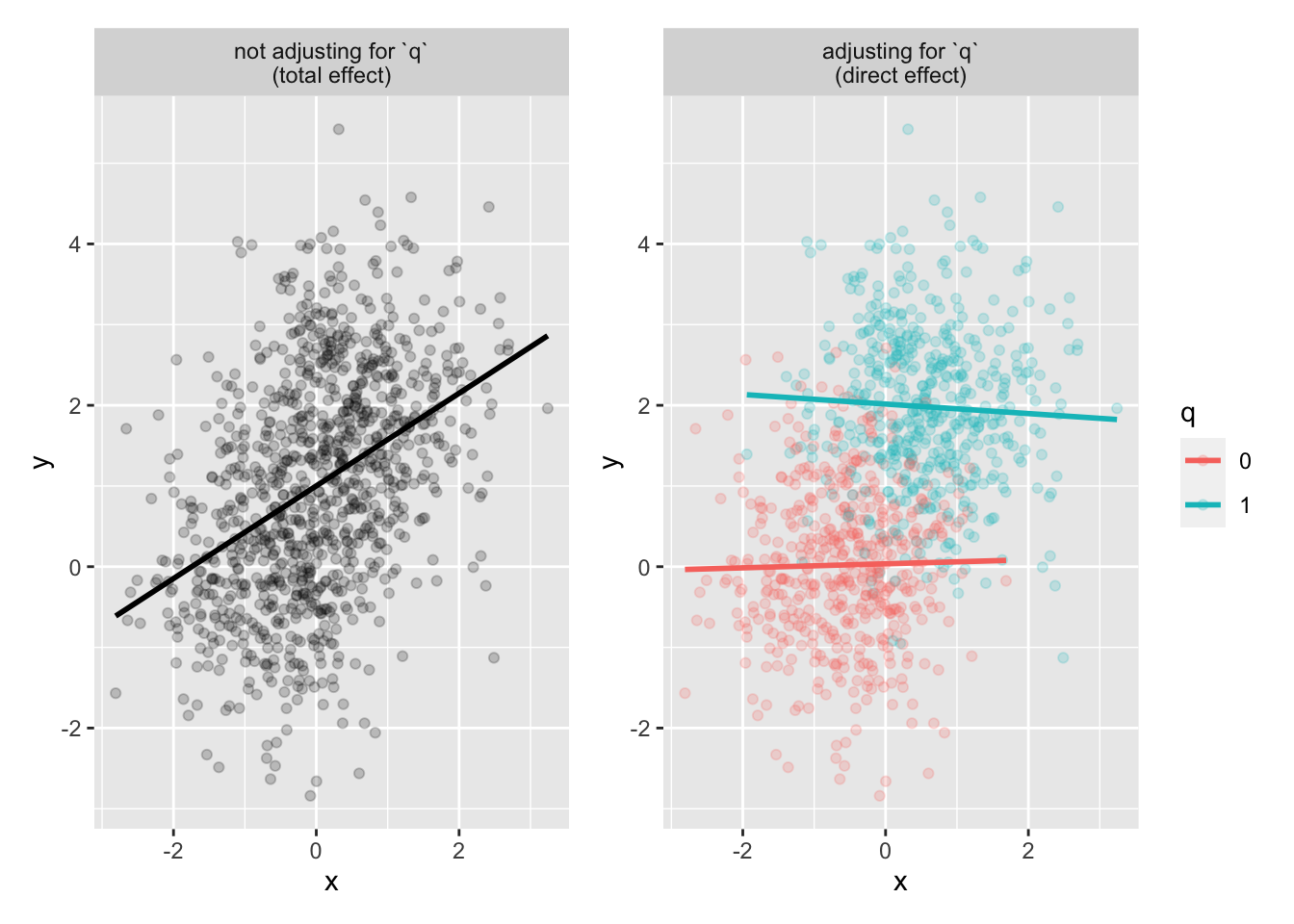

Corr

lares::corr_cross(mediator_data)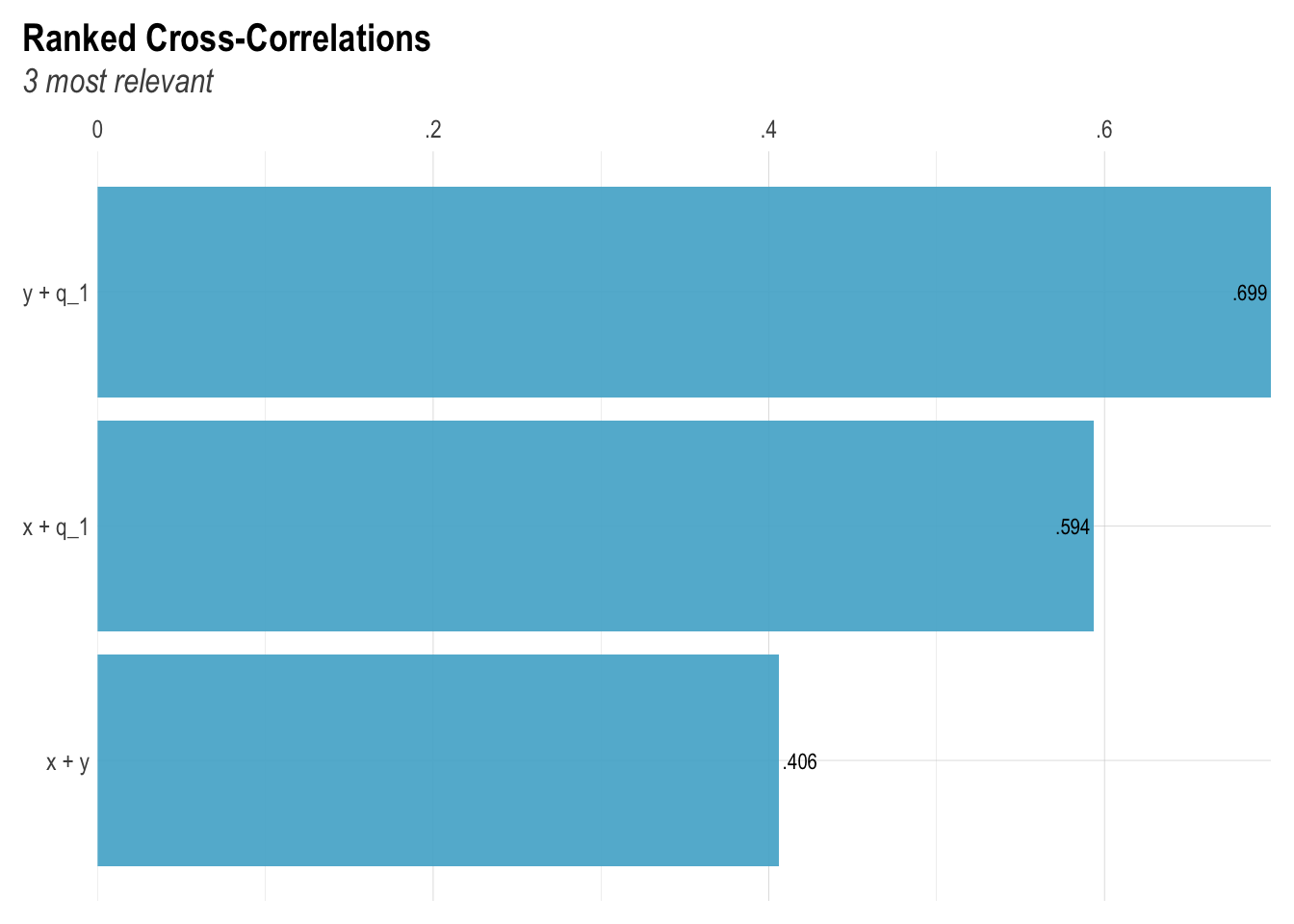

correlation(mediator_data)

# Correlation Matrix (pearson-method)

Parameter1 | Parameter2 |    r |       95% CI | t(998) |         p
------------------------------------------------------------------
x          |          y | 0.41 | [0.35, 0.46] |  14.04 | < .001***

p-value adjustment method: Holm (1979)
Observations: 1000

Model

# Not Adjust
## y ~ x
mediator_data.fit.y_x <- lm(y ~ x, data = mediator_data)
## y ~ q 
mediator_data.fit.y_q <- lm(y ~ q, data = mediator_data)
## x ~ q
mediator_data.fit.x_q <-  lm(x ~ q, data = mediator_data)

# Adjusted: y ~ x + q 
mediator_data.fit.y_xq <- lm(y ~ x + q, data = mediator_data)

Code

mediator_data.fit.tbls <- 
  list(
    y_x = mediator_data.fit.y_x,
    y_q = mediator_data.fit.y_q,
    x_q = mediator_data.fit.x_q,
    y_xq = mediator_data.fit.y_xq
  ) |> 
  map(tbl_regression_custom)
  
mediator_data.fit.tbls |> 
tbl_merge(
  tab_spanner = c("**y ~ x**", "**y ~ q**", "**x ~ q**", "**y ~ x + q**")
  )

Characteristic	y ~ x			y ~ q			x ~ q			y ~ x + q
Characteristic	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value
x	0.57	0.49, 0.65	<0.001							-0.02	-0.10, 0.06	0.622
q
0				—	—		—	—		—	—
1				2.0	1.8, 2.1	<0.001	1.2	1.1, 1.3	<0.001	2.0	1.8, 2.1	<0.001
¹ CI = Confidence Interval

Collider (Bias)

Sim Data

set.seed(1)
x <- rnorm(n)
y <- rnorm(n)

linear_pred <- 2 * x + 3 * y + rnorm(n)
prob <- 1 / (1 + exp(-linear_pred))
q <- rbinom(n, size = 1, prob = prob)

collider_data <- tibble(x, y, q = as.factor(q))

Plot

Code

p1 <- collider_data |>
  ggplot(aes(x, y)) +
  geom_point(alpha = .2) +
  geom_smooth(method = "lm", se = FALSE, color = "black") +
  facet_wrap(~"not adjusting for `q`\n(unbiased)")

p2 <- collider_data |>
  ggplot(aes(x, y, color = q)) +
  geom_point(alpha = .2) +
  geom_smooth(method = "lm", se = FALSE) +
  facet_wrap(~"adjusting for `q`\n(biased)")

p1 + p2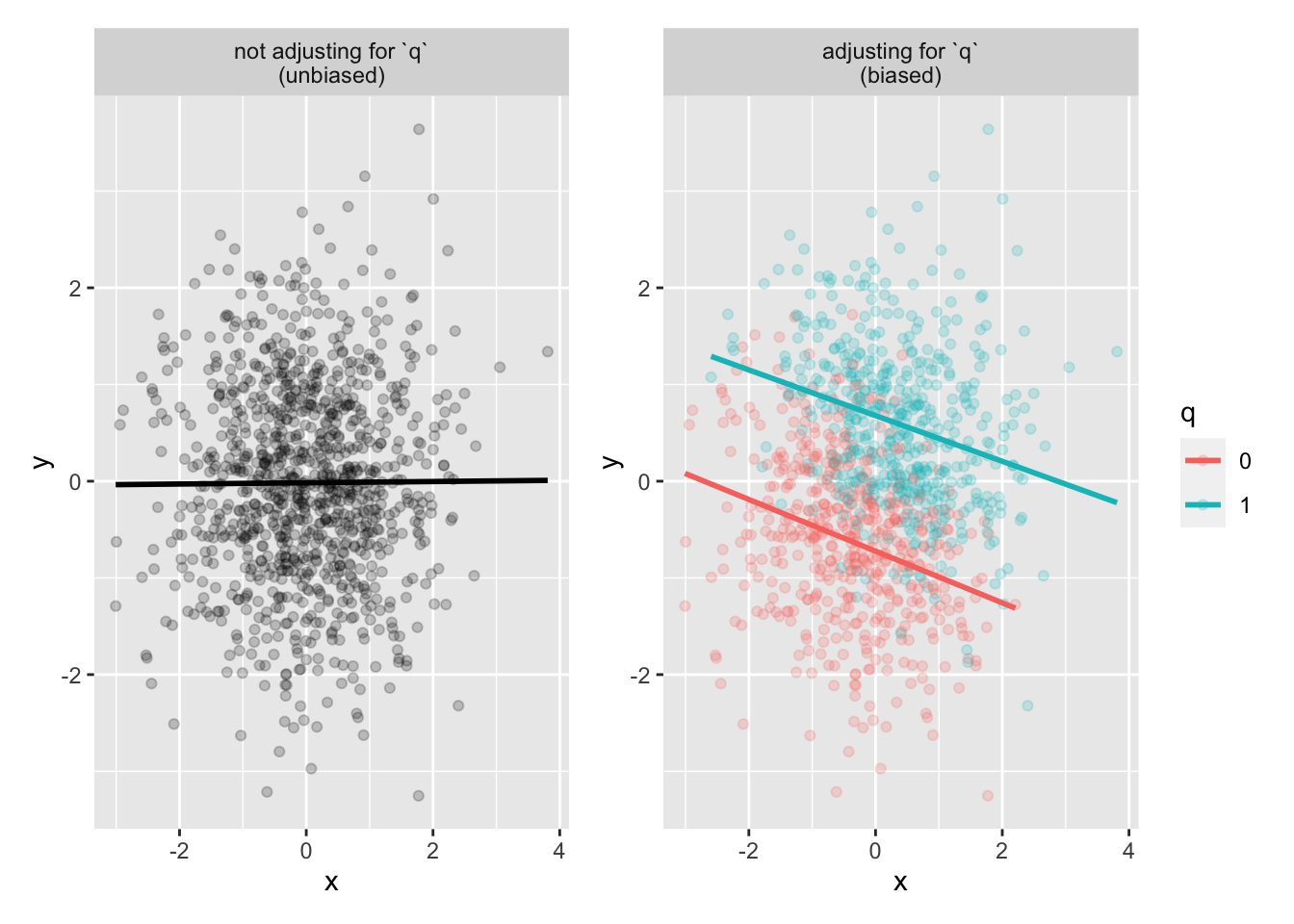

Corr

lares::corr_cross(collider_data)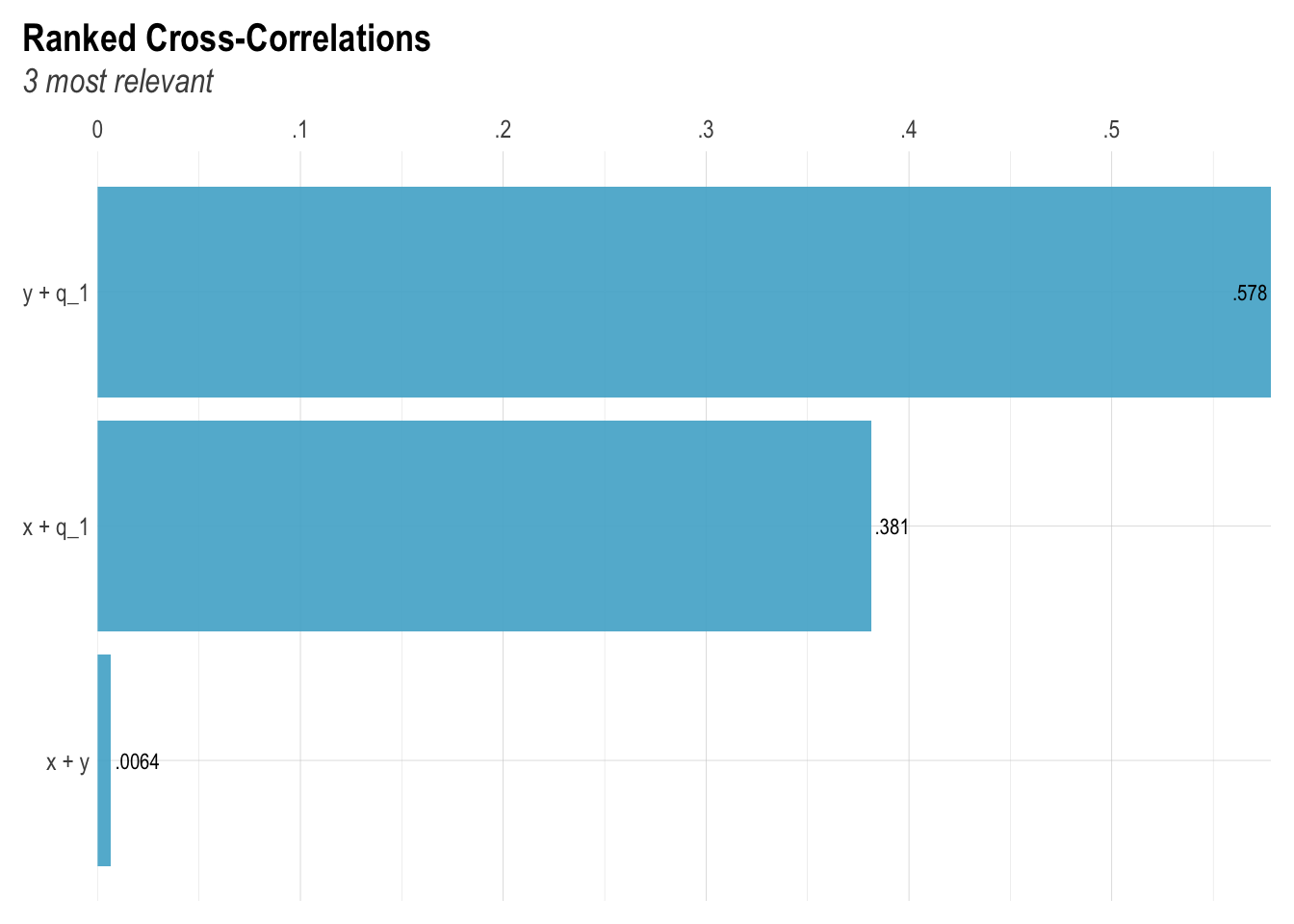

correlation(collider_data)

# Correlation Matrix (pearson-method)

Parameter1 | Parameter2 |        r |        95% CI | t(998) |     p
-------------------------------------------------------------------
x          |          y | 6.40e-03 | [-0.06, 0.07] |   0.20 | 0.840

p-value adjustment method: Holm (1979)
Observations: 1000

Model

# Not Adjust
## y ~ x
collider_data.fit.y_x <- lm(y ~ x, data = collider_data)
## y ~ q 
collider_data.fit.y_q <- lm(y ~ q, data = collider_data)
## x ~ q
collider_data.fit.x_q <-  lm(x ~ q, data = collider_data)

# Bias: y ~ x + q 
collider_data.fit.y_xq <- lm(y ~ x + q, data = collider_data)

Code

collider_data.fit.tbls <- 
  list(
    y_x = collider_data.fit.y_x,
    y_q = collider_data.fit.y_q,
    x_q = collider_data.fit.x_q,
    y_xq = collider_data.fit.y_xq
  ) |> 
  map(tbl_regression_custom)
  
collider_data.fit.tbls |> 
tbl_merge(
  tab_spanner = c("**y ~ x**", "**y ~ q**", "**x ~ q**", "**Bias: y ~ x + q**")
  )

Characteristic	y ~ x			y ~ q			x ~ q			Bias: y ~ x + q
Characteristic	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value	Beta	95% CI¹	p-value
x	0.01	-0.06, 0.07	0.840							-0.25	-0.30, -0.20	<0.001
q
0				—	—		—	—		—	—
1				1.2	1.1, 1.3	<0.001	0.79	0.67, 0.91	<0.001	1.4	1.3, 1.5	<0.001
¹ CI = Confidence Interval

Summary

Significant coefficient by correlation, simple and multiple LM